String-theoretical understanding of orderly relationships (coherence)

Position paper by B. Zeiger
using AI supported internet searches (ChatGP
(October 31, 2024)"The Paramatman Light
is everywhere and in everything."

Mother Meera

The impetus and starting point for this position paper is the observation that many U(1) fields occur frequently and naturally in string theories. Anyone who deals theoretically with the phenomenon of light knows that the electromagnetic radiation field, colloquially known as light, is also a U(1) field.

In classical physics, the electromagnetic U(1) field determines the forces that govern the behavior of matter. Light, which is based on this field, is of fundamental importance for life on earth and influences almost every aspect of biological processes as well as the behavior of living beings on earth:

Light is a source of energy - a timer and regulates biological rhythms: - Orientation aid - habitat - means of communication - means of perception - motor for growth, evelopment: and evolution and much more

The question arises as to what extend the string-theoretical U(1) fields (i.e. field structures similar to the electromagnetic potential in the space-time world) occurring in higher dimensions are responsible for the structure of the universe and the emergence, development and existence of life.

In string theory, the function of the U(1) fields is more comprehensive. The higher dimensional "light" as a generalized field structure or vibrational pattern explains not only electromagnetic but also other physical interactions. The higher dimensions postulated in string theory can give rise to additional forms of symmetry and interaction which, although not directly observable, are fundamental to the structure and stability of the universe.

This may have implications for life:

Fundamental interactions and stability of matter: Higher dimensional U(1) fields could provide an explanation for the stability and symmetry of matter. Just as visible light and electromagnetic fields are essential for biological processes, such fields in higher dimensions could fundamentally determine the structure of our reality by defining the physical laws and constants that make life possible.
The potential to explain dark energy or dark matter: Since higher dimensions and their field structures may involve particles and forces that do not act directly in our three-dimensional space, they could explain phenomena such as dark matter or dark energy - phenomena that make up more than 95% of the universe and therefore certainly play a significant role in the cosmic balance and structure of the universe and thus probably also have an indirect influence on life.
Relation to consciousness: Some hypotheses within string theory approaches, suggest that higher-ion fields could influence interactions that operate beyond the known four dimensions of space and time) and perhaps even affect consciousness or subjective perception.

All of this is currently still highly speculative, but it is at least conceivable that such U(1) fields in the higher dimensions of string theory are important for the existence, further development and behavior of the material structures and life forms known to date.

There are a few contemporary physicists and authors who are seriously considering, or at least have expressed thoughts on, the idea that the higher dimensional "light" fields of string theory might play a role in life as part of their scientific work:

Michio Kaku: The theoretical physicist and co-founder of string field theory has speculated that the higher dimensions of string theory could provide deeper insights into the universe and perhaps even into consciousness. In popular science books, he describes how higher dimensions could be the foundation of our reality and how these dimensions could influence the structure and existence of life.
Leonard Susskind: One of the co-founders of string theory and holographic principles, has suggested in his work that higher dimensions and holography could possibly form a kind of "blueprint" of the universe. His work shows how the structure of the universe is shaped by higher dimensional principles. Susskind has focused more on the principles of the holographic universe and quantum gravity. His work is on the relationship between information, spacetime and gravity. The importance of U(1) symmetry as a field structure is therefore treated as part of a larger theoretical framework, not as a standalone concept.
John Archibald Wheeler: Although not yet a string theorist, Wheeler was a theoretical physicist and cosmologist, but he developed the concept of "It from Bit", which suggests that information (perhaps in the form of quantum fields or higher dimensions) could be the basis of reality and life. Wheeler's ideas have inspired many string theorists to consider the role of higher-dimensional structures.
Edwin Witten: As one of the most prominent theorists in string theory, Witten has worked extensively with U(1) fields and symmetries, particularly in the context of superstring and M-theory. U(1) symmetries are an integral part of his work on gauge fields and supersymmetries, particularly in the context of anomaly cancellation and force unification. However, his work focuses on mathematical and physical foundations rather than on speculative aspects or the role of these fields in a biological sense.
Lisa Randall: Theoretical physicist Lisa Randall has worked on concepts of higher dimensional spaces, particularly in the context of brane theory. She speculated that these dimensions, although invisible, might possess a physical reality that could subtly influence gravity and possibly the existence of biological life. Randall is known for her work on extra-dimensional models such as brane theory (e.g. the Randall-Sundrum model), in which U(1) fields behave on the so-called branes and their interactions take place mainly in the 4D world. She explains how U(1) fields in extra dimensions could lead to new interactions, but she does not explicitly connect the concept to topics such as life or consciousness.
Heinrich Päs: Physicist Heinrich Päs, particularly in his book The ONE, deals with the metaphysical implications of modern physics, including higher dimensions and the role of consciousness. He investigates whether the universe might have a "spiritual" foundation, with U(1) fields or higher dimensions playing a role if reality and consciousness are considered to be interconnected.

However, the development of string theory, which was still perceived as revolutionary in the second half of the 20th century, stalled at the beginning of the 21st century. Theorists such as H. Päs therefore state that physics is in crisis. In his book The ONE, published in 2023, he analyzes the situation of string theory research and the extent to which its mathematical structures may describe more than just objective physical reality. For H. Päs, string theory is the first step towards a more comprehensive worldview that includes both the physical and the spiritual world. He sees in it the potential for a new, integrative perspective on science and philosophy that integrates consciousness and subjective experience into a scientific model. Päs advocates using the knowledge of the unity of the world handed down by ancient cultures to overcome the crisis; so that physical reality and consciousness are no longer separate entities, but manifestations of a single, fundamental "being".

This position paper takes up the approach of H. Päs, and incorporates the insights and proven methods of ancient Vedic culture, especially meditation. According to traditional Vedic literature, certain steps are always taken to gain an exact understanding of reality. As Maharishi Mahesh Yogi explained in his commentary on the Bhagavad Gita (Chapter 2), Vedic science distinguishes five steps of understanding:

Understanding the changeable and the unchangeable,
Understanding the force of evolution,
Understanding relationships,
Understanding the freedom of choice and the effects of activity,
Understanding the uninvolved absolute reality of the actor

The following chart gives an overview of how, according to this step-by-step approach, the stringtheoretical relationship between light and consciousness can become the lived reality of each individual by virtue of unitary transformations.

The program summarized in the chart requires some explanation. The Sanskrit terms used in the chart are intended to point out the important distinction between "description of a reality" (string theory) and "reality itself" (Sanskrit expressions). In a description using mathematics, for example, terms such as "transformation" or "mapping" and "reference system" appear, while reality itself is characterized by changes (light of consciousness) in the underlying unchanging substance (Paramatman). This corresponds to the difference between a map and a land. Descriptions are man-made, while reality is autonomous and exists independently, but also includes humans. What connects everything is consciousness in its simplest form.

From an academic point of view, the chart links philosophical ideas from the Vedic tradition with the formal and epistemological aspects of string theory. Although this opens up an interesting interdisciplinary perspective, it takes some getting used to for academically trained scientists, because physics, and thus also string theory, is primarily about mathematical models and empirical predictions about the nature of reality, without addressing metaphysical or meditative states of consciousness.

But there are important reasons for linking both areas - modern physics and Vedic wisdom:

The need for new perspectives on knowledge: Since string theory has so far offered no empirically verifiable predictions, some physicists and philosophers are looking for new ways to interpret and apply it. A connection to the study of consciousness could offer a new perspective, that is not necessarily physically experimental, but epistemologically and metaphysically accessible.
If the mathematical structure of the universe is seen as an expression of a deeper consciousness, string theory could provide a bridge to the metaphysical exploration of consciousness
Relationship between consciousness and reality:
Quantum theory shows that the observer plays an essential role in determining the state of a system, since the state of a particle remains "entangled" i.e. in a state of superposition of possibilities until it is measured. Since string theory is an extension of quantum theory, it can be assumed that it could offer even more precise insights into the relationship between consciousness and reality. String theory could perhaps provide a mathematical basis to describe how the physical and the mental might interact, which would deepen the understanding of subjective reality and its relationship to objective reality (mind-body problem)

Some researchers therefore view string theory as a potentially deeper framework that could encompass more than physical reality. Theoretical concepts such as "holography" or the "quantum information paradigm" have parallels with the way states of consciousness and subjective experiences could be modeled, for example through information processing. Approaches in this direction can be found in Edward Witten, Juan Maldacena, Leonard Susskind, Roger Penrose and most recently in H: Päs. However, it is important to clarify:

String theory itself makes no statements about consciousness or meditation: its approaches are formal mathematical models. This requires a deep mathematical intuition, but this alone does not guarantee spiritual insight. The formal, mathematically precise methods of string theory function largely independently of the individual's state of consciousness.
In order for the "light of pure consciousness" to also include the world of string theor, this presupposes the existence of pure consciousness in the nervous system as its collectively coherent ground state or state of being. Without the existence of the conscious state of being (I-ness), conceptual images (strings) cannot be related to it.
It is the practice of meditation that creates a connection between mental concepts and pure self-related consciousness (Paramatman). Without the practice of meditation, formal systems, isms, beliefs, dogmas, postulates or axioms have no consciousness-related meaning.
Only when a connection between pure consciousness and mental concepts is created or exists through meditation can the light of consciousness become effective in an orderly manner. Talking about the light of pure consciousness does not create this connection.
The mere mental, purely formal engagement with string theory alone is not enough for the light of pure consciousness to understand the foundations of progress - stability, flexibility, Integration, purification and growth – enlivened in the world.

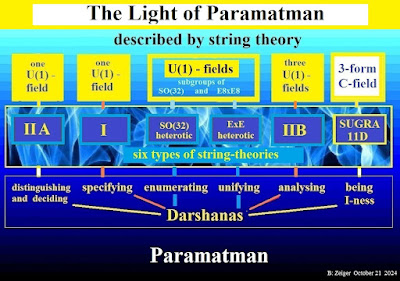
According to the practical insights of Vedic culture, the inflow of the light of pure consciousness occurs through psycho-physiological processes known as darshanas. Meditation is one of them. Vedic tradition summarizes all of this process in 6 systems Nyaya, Vaiseshika, Samkhya, Yoga, Karma Mimansa and Vedanta, which refer to 6 qualities of intelligence according to the meanings of the respective Sanskrit terms: distinguish and decide, specify, enumerate, unify, analyze and to be.

In order to understand the relationship between darshanas and string theory, the 5 steps of understanding mentioned above are required, which in string theory concern the following topics:

1. Interplay of relative and absolute reality,
2. Steps of holistic development: quantization.
3. Interactions and gauge fields
4. The semi-classical view: string theory and darshanas
5. Self-reference and unitary transformation

(The detailed elaborations of these topics are available on request as PDF files: Email dr.zeiger@t-online.de).

The first step to understand why the U(1) fields play a major role as representatives of light is to know what the abbreviation U(1) means and what consequences can be derived from it:

U(1) stands for one-parameter unitary transformations, i.e. for transformations that are, on the one hand, characterized by only one specific feature (e.g. charge or angle of view) and, on the other hand, change the perspective of the entire reality only with regard to this one specific feature, without affecting the structure of reality as a whole. Hence the term unitary. Because of this self-reference, unitary transformations characterize a reality that, as I. Kant recognized, is the prerequisite for knowledge and experience to be possible in the first place.

The term U(1) fields therefore includes the self-referential character of reality, and thus its relationship to cognition and perception. Unitary transformations therefore characterize the underlying reality because of its self-referentiality as consciousness. The most elementary characteristic of consciousness is self-reference.

The eponymous feature of string theory is that it describes the underlying multidimensional reality as a collection of vibrating threads (strings) and no longer as a totality of space-time points (events) like classical physics.

String theory is based on certain fundamental axioms and assumptions, even if it is not formally as strictly structured as other theories. The essential "axioms" of string theory are, in simple terms:

All matter and forces are "strings": The fundamental building blocks of the universe are not particles (like electrons or quarks), but tiny, vibrating threads called "strings." Depending on the way these strings vibrate, they appear to us as different particles.
Strings exist in higher dimensions: To be mathematically consistent, string theory requires more than the usual four dimensions (three spatial dimensions and one time dimension). The exact dimensions vary depending on the type of string theory, but are most often 10 or 11. These extra dimensions are often "rolled up" and not directly visible.
Unification of the fundamental forces: String theory strives to describe all known forces - the electromagnetic, weak, strong and gravitational forces - in a unified theory. This means that these forces are different manifestations of the same fundamental structure mediated by strings.
Supersymmetry (SUSY): Most versions of string theory involve supersymmetry, an organizing principle that states that every particle has a particle as a "superpartner". This symmetry is important to keep the theory mathematically consistent and to help unify the forces.

The method of string theory then consists in describing these strings holistically using unitary transformations and then looking at the classical reality of space-time from this perspective. Put simply, string theory sees classical reality from a quantum mechanical perspective. String theory therefore makes it possible to understand the reality underlying everything in more detail than was previously possible.

Thus String theory describes the classical space-time world from a quantum mechanical perspective by replacing the concept of point-like particles with vibrating, one-dimensional objects - strings. These strings are the fundamental "building blocks" of reality, and their vibrational states determine the properties of all particles and forces that we observe. The essential aspects of string theory are:

Quantized space-time: String theory treats space and time not as a static stage, but as dynamic entities that are co-determined by the interactions of the strings. This means that space and time themselves are influenced by the vibrations and interactions of the strings, so that the classical space-time world is viewed as an emergent structure from a deeper quantum mechanical reality.

Unitary transformations and symmetries: In string theory, the states of the strings are connected to each other by unitary transformations, which ensures that the probabilities (the squares of the amplitudes) are preserved and the theory remains consistent. These transformations form the basis for quantization and for the symmetries that describe the fundamental forces and particle properties, such as the U(1) symmetry for the electromagnetic field. String theory tries to unify all symmetries and interactions in a unified framework.
The "underlying reality": By describing the strings as vibrational modes of different types of particles and forces, a deeper, unified reality is postulated from which both matter and the geometry of spacetime itself emerge. This means that the properties of the classical space-time world are ultimately understood as an expression of these quantum mechanical string dynamics.
Higher dimensions and detailed structure: By introducing additional spatial dimensions (10 or 11 depending on the theory) and symmetric fields, the structure of the underlying reality is differentiated even further. String theory allows for a more detailed description that attempts to explain all known interactions and particles, including those that do not occur in classical physics, such as gravity in the quantum system.

String theory therefore looks at the space-time world and its contents through a quantum mechanical lens, in which the objective reality of space-time emerges from the dynamics and interactions of strings and their symmetries, including unitary transformations. It thus provides the basis for a detailed description of reality that also includes the classical space-time world as an emergent phenomenon.

Appendix

The purpose of this appendix is to provide a link to the paper on the "Life Relevance of Unifying Consciousness".

U(1) Fields and Light Cones

1, The Role of U(1) Symmetry in String Theory

The U(1) symmetry plays a central role in string theory because it is the simplest form of a so-called "gauge symmetry", which is essential for understanding fundamental interactions. In physics, the U(1) symmetry is the mathematical basis for electromagnetic interaction, i.e. quantum electrodynamics (QED).
In string theory, there are several types of gauge symmetries, including U(1), SU(2), and SU(3). The U(1) fields are actually the simplest of these fields:

Simplicity of U(1) fields: U(1) fields are the simplest because they only describe a single charge (like the electric charge). They are simpler than more complex fields such as SU(2) or SU(3), which are responsible for the weak and strong nuclear forces, respectively, and describe several charges or color charges.
Application to electromagnetic interactions: In string theory and other quantum field theory approaches, U(1) symmetries form the basic model for the electromagnetic interaction mediated by the photon. This U(1) symmetry is often the starting model for describing other, more complicated symmetries.
Embedding in larger symmetries: In some versions of string theory, especially in heterotic string theory (e.g. E8×E8 theory), the U(1) symmetry is embedded in larger, multidimensional symmetry groups. This means that the U(1) fields appear here as a partial aspect of a more comprehensive structure that brings together several fundamental interactions.

So overall it can be said that U(1) fields are the simplest fields in string theory, describing basic interactions such as the electromagnetic force. In more complex string theories they form the basis for moving on to more complex structures that model multiple forces and properties of matter.

2, The light cone in string theory

In string theory, the light cone represents the limit for causal interactions, i.e. the range within which events can influence each other, similar to the theory of relativity. This limit also applies to strings: a signal or interaction between strings can only take place within the light cone of a certain point in space and time.

The concept of a "light cone" can therefore in principle also be generalized to the higher dimensions of string theory. In general relativity, the light cone describes the area in space-time that a light beam can reach from an event (future cone) or from which it could come (past cone). In string theory and other higher-dimensional theories, a similar concept of signal behavior and causality may exist.

Light cone in higher-dimensional spacetimes: In theories with more than four dimensions (e.g. 10 or 11 dimensions in string theory and M-theory), the light cone can be extended to additional spatial dimensions. This higher-dimensional light cone then describes not only the boundaries in the known four dimensions, but also in the additional dimensions in which signals, particles or strings could theoretically move.
Causality and event relationship in higher dimensions: The light cone determines which events can be causally related. In higher dimensions, such causal relationships could change. For example, events that appear separate in four dimensions could be connected in a higher dimension. This has implications for the concept of time and causal order, since the universe in a higher dimension could have more complex connections and interactions between events.
Holographic principles and projections: In string theory, there are theories that propose that our four-dimensional reality could be a "hologram" of a higher-dimensional space-time (Holographic principle). In this case, the light cone in our four-dimensional space-time could be a projection of a higher-dimensional "light cone", with certain aspects of our causality originating from these higher dimensions.
Effects on the perception of space and time: If we perceived the additional dimension as accessible and real, the light cone could also have "lateral" components showing movements or signals in the direction of these dimensions. This would mean that the propagation of light or of signals in general is influenced by higher space-time references.
Hypothetical role for "dark" interactions: There is speculation that dark matter or dark energy could be explained as effects of higher-dimensional causal structures that we can only measure indirectly due to our limited perception in four dimensions. The propagation of a signal in a higher dimension could modify the gravitational interaction that we observe in our "normal" light cone.

The generalization of the light cone to higher dimensions in string theory means that causality may also be influenced by additional dimensions invisible to us, making the structure of space and time more complex and potentially allowing for new types of causal connections or “hidden” interactions.

3. Relationship between light cone and U(1) field in quantum electrodynamics and string theory

In quantum electrodynamics (QED) and string theory, there is a close relationship between the light cone and the U(1) field, especially in terms of describing the electromagnetic field and its propagation.

3.1 Quantum electrodynamics (QED)

U(1) field and electromagnetism: In QED, the U(1) symmetry describes the electromagnetic field mediated by the photon as the interacting particle. The U(1) symmetry stands for the invariance of the electromagnetic interaction under phase transformations of the wave function.
Light cone and causality: The light cone defines the boundaries of causality in the space-time continuum. Events within the light cone of a given point can be causally related, while events outside the light cone are beyond the reach of electromagnetic interactions, since light only travels at a finite speed (the speed of light).
Relationship between light cone and U(1) field in QED: The U(1) field and its quantization describe the propagation of photons within the light cone. Electromagnetic interaction can only be exerted within the light cone, since photons - the carriers of the U(1) field - propagate at the speed of light. Therefore, the light cone in space-time determines how far the U(1) field in QED can transmit a signal or force.

3.2 String theory

Strings and U(1) fields: In string theory, U(1) fields can be understood as special vibrational states of strings that describe electromagnetic interactions. In string theory, the U(1) field is also associated with photons and electromagnetic forces, but here it results from the fundamental vibrations of a string.

Light cone and propagation in higher dimensions: In string theory, the light cone expands to higher dimensions. This means that strings carrying U(1) fields (e.g. electromagnetic interactions) could potentially propagate in these additional dimensions. The shape and structure of the light cone would thus not be limited to the classical four dimensions. For observers in four dimensions, however, only the projections of these interactions remain visible, which gives us a limited view of the effect of the U(1) field.
Causality and the holographic context: In string theory approaches such as the AdS/CFT correspondence, light cones and causality are also considered via so-called holographic principles, where a higher-dimensional reality is projected onto the known dimensions. Here, the U(1) symmetry remains a fundamental role for describing electromagnetic and possibly other interactions, but the extension of the light cone in higher dimensions and its projection can lead to interesting causal structures.

In both theories, the U(1) field describes electromagnetic interactions and their propagation, which are oriented to the boundaries of the light cone. The light cone determines where the electromagnetic force can act in space and time, as it determines the boundaries of causality in both theories. In string theory, however, the light cone could be extended by additional dimensions and holographic projections, which could affect the structure of the U(1) field and possibly imply new causal relationships.